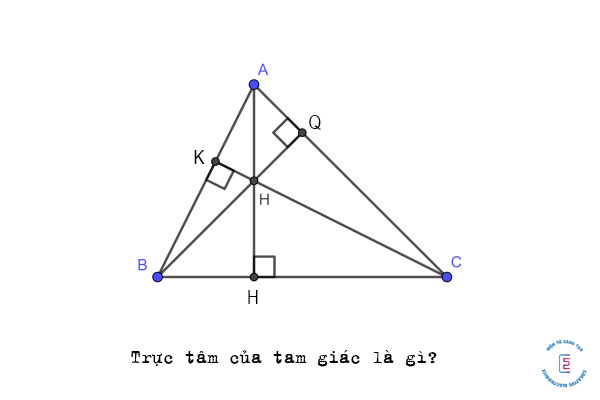
Trực tâm của tam giác là gì? Tính chất của trực tâm trong tam giác ra sao? Hãy cùng chúng tôi tìm hiểu thông tin trong nội dung dưới đây của bài viết để tìm lời giải đáp
Trực tâm của tam giác là gì?
Trực tâm của tam giác là giao điểm của 3 đường cao tương ứng với 3 đỉnh của 1 tam giác. Mỗi tam giác chỉ có 1 trực tâm duy nhất và trực tâm đó có thể nằm bên trong hoặc bên ngoài miền của tam giác.
Đường cao tương ứng của mỗi đỉnh tam giác được biết đến là một đường thẳng nối từ đỉnh đến cạnh đối diện và vuông góc với cạnh đối diện tại điểm cắt. Cạnh đối diện diện được gọi là cạnh đáy tương ứng với chính đường cao đó.
Độ dài của đường cao sẽ được định nghĩa là khoảng cách giữa phần đỉnh và đáy tương ứng của nó.
Bạn có thể hình dung đơn giản như sau, giả sử cho 1 tam giác ABC với 3 đường cao lần lượt là AH, BQ và CK. Gọi S là giao điểm của 3 đường cao trên thì S cũng chính là trực tâm của ∆ABC.
Tính chất trực tâm của tam giác
Như các bạn cũng đã biết thì trực tâm tam giác có khá nhiều các định lý và tính chất quan trọng. Muốn thực hiện được các dạng bài tập thì bắt buộc cần phải nắm rõ được các định lý và những tính chất này thì mới có thể giải được các bài tập nhanh chóng và hiệu quả.
Trong trường hợp 3 đường cao của tam giác đi qua cùng 1 điểm thì điểm đó sẽ gọi là trực tâm của tam giác. Khoảng cách giữa tâm đường tròn ngoại tiếp tam giác đến trung điểm của 2 cạnh sẽ bằng ½ khoảng cách từ trực tâm đến đỉnh còn lại của tam giác đó.
Đối với tam giác cân thì đường trung trực tương ứng với cạnh đáy thông thời sẽ là đường cao, đường trung tuyến của tam giác đó. Trong 1 tam giác nếu đường trung tuyến đồng thời là đường phân giác thì tam giác đó chính là tam giác cân.
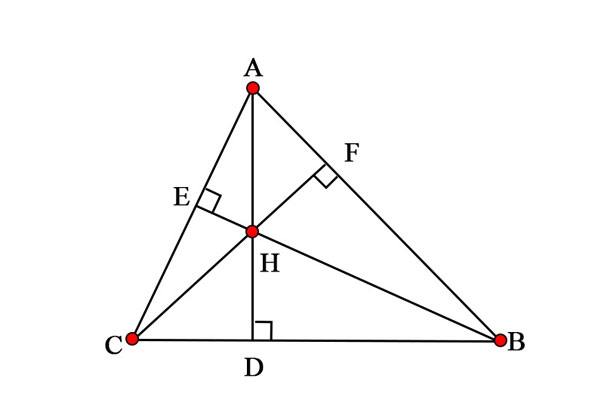
Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác được tạo bởi 3 đỉnh là chân đường cao tương ứng với 3 đỉnh của ∆ABC.
Định lý Carnot chỉ rằng đường cao tương ứng với 1 đỉnh của tam giác và cắt đường tròn ngoại tiếp tam giác ở đâu thì điểm đó sẽ chính là điểm đối xứng với trực tâm tam giác đó quá chính cạnh đáy đối xứng của đỉnh.
Từ những tính chất ở trên thì ta có thể rút ra hệ quả như sau: Trong một tam giác đều thì trực tâm, trọng tâm, điểm nằm trong tam giác, điểm cách đều 3 đỉnh của tam giác và cách đều 3 cạnh thì 4 điểm này sẽ đều trùng nhau là một điểm.
Bạn có thể tóm lại 5 tính chất trực tâm của tam giác như sau:
- Trong tam giác cân thì đường trung trực sẽ tương ứng với các cạnh đáy sẽ đồng thời là đường cao, đường trung tuyến, đường phân giác của tam giác đó.
- Trong 1 tam giác, nếu đường trung tuyến đồng thời là đường phân giác thì tam giác đó sẽ là tam giác cân.
- Trong 1 tam giác, nếu đường trung tuyến đồng thời là đường trung trực thì tam giác đó cũng được gọi là tam giác cân.
- Trực tâm của ∆ABC nhọn sẽ trùng với tâm của đường tròn nội tiếp tam giác với 3 đỉnh là chân của 3 đường cào từ đỉnh A, B, C đến các cạnh đối diện tương ứng. AB, AC và BC.
- Đường cao của tam giác ứng với mỗi đỉnh sẽ cắt đường tròn ngoại tiếp tại 1 điểm thứ 2 sẽ là đối xứng của trực tâm qua cạnh tương ứng.
Các cách xác định trực tâm của tam giác
Trực tâm của tam giác vuông
Tam giác vuông KML có trực tâm H trùng với góc vuông K
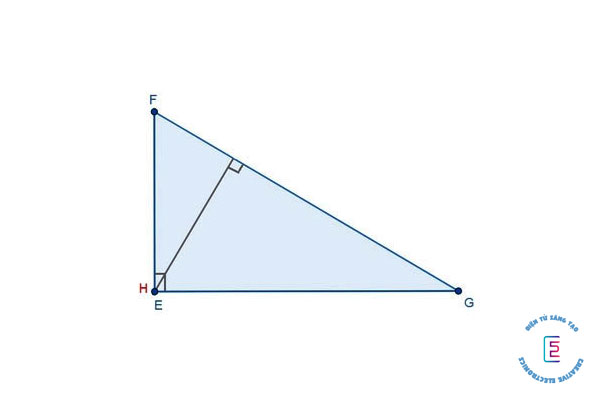
Trực tâm của tam giác nhọn
Tam giác nhọn EFG có trực tâm là H nằm ở miền trong của tam giác
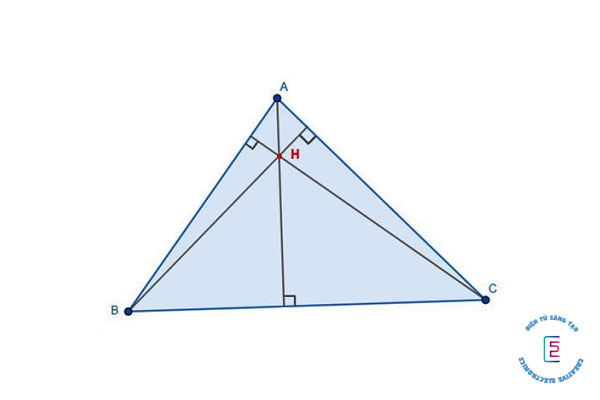
Trực tâm của tam giác tù
Tam giác tù CDE có trực tâm H nằm ở miền ngoài tam giác
Các bài tập ứng dụng trực tâm của tam giác
Bài tập 1: Cho ΔABC, hai đường cao BD và CE. Gọi M là trung điểm của BC. Em hãy chọn câu sai:
- ME = MD
- DM = MB
- BM = MC
- M không thuộc đường trung trực của DE
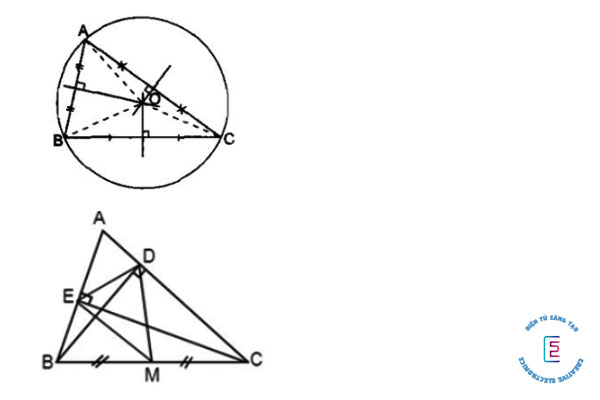
Vì M là trung điểm của BC (gt) suy ra BM = MC (tính chất trung điểm), loại đáp án A.
Xét ΔBCE có M là trung điểm của BC (gt) suy ra EM là trung tuyến
⇒ EM = BC/2 (1) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Xét ΔBCD có M là trung điểm của BC (gt) suy ra DM là trung tuyến
⇒ DM = MB = BC/2 (2) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C
Từ (1) và (2) ⇒ EM = DM ⇒ M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D
Đáp án D – Đúng: M không thuộc đường trung trực của DE
Bài tập 2: Cho ΔABC cân tại A, hai đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔMED là tam giác gì?
- Tam giác vuông cân.
- Tam giác vuông.
- Tam giác cân.
- Tam giác đều.
Đáp án: C Đúng – Tam giác cân
Bài tập 3: Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).
Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Chứng minh KN ⊥ IM.
Lời giải:
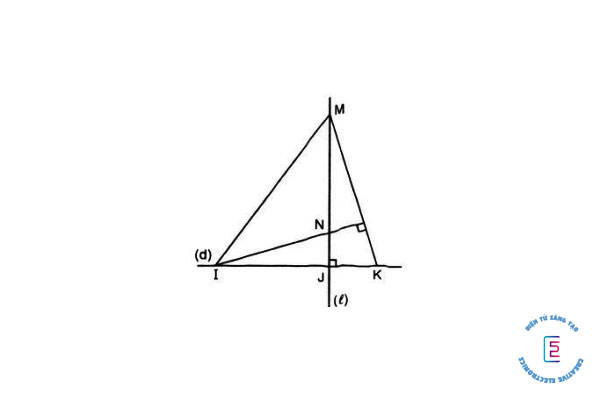
Trong một tam giác, ba đường cao đồng quy tại một điểm là trực tâm của tam giác đó.
l ⊥ d tại J, và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.
N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.
IN và MJ cắt nhau tại N .
Theo tính chất ba đường cao của tam giác ⇒ N là trực tâm của ΔMKI.
⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.
Vậy KN ⏊ IM
Bài tập 4: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
- a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
- b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
Lời giải:
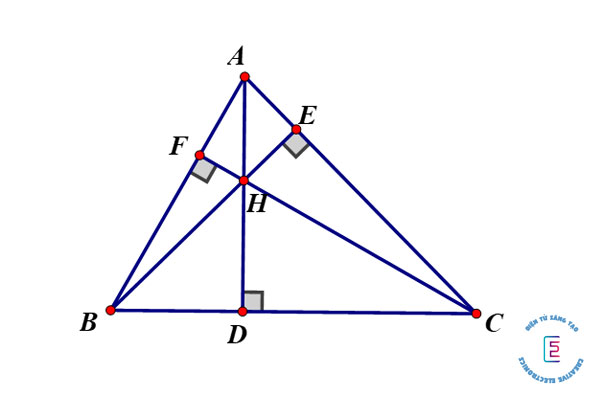
a) ΔHBC có :
- AD ⊥ BC nên AD là đường cao từ H đến BC.
- BA ⊥ HC tại F nên BA là đường cao từ B đến HC
- CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
- AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.
b) Tương tự :
- Trực tâm của ΔHAB là C (C là giao điểm của ba đường cao : CF, AC, BC)
- Trực tâm của ΔHAC là B (B là giao điểm của ba đường cao : BE, AB, CB)
Trực tâm của tam giác là gì? Tính chất trực tâm của tam giác ra sao? Câu hỏi đã được chúng tôi giải đáp đến bạn và cũng đã có những bài tập tham khảo. Hy vọng với những thông tin trên sẽ giúp ích cho bạn trong học tập.