Trong bài viết này chúng tôi sẽ chia sẻ đến bạn công thức tính thể tích hình trụ và các bài tập liên quan, để bạn có thể tham khảo và áp dụng để giúp giải các bài tập một cách hiệu quả. Mọi thông tin bạn có thể tham khảo nội dung phía dưới của bài viết.
Công thức tính thể tích hình trụ
Như các bạn cũng đã biết thì hình trụ tròn là hình có 2 mặt đáy là 2 hình tròn song song và bằng nhau. Ngoài thực tế, bạn có thể bắt gặp rất nhiều các vật dụng với hình dạng là hình trụ như cái cốc, hộp sữa, lon bia,… Cách tính thể tích của hình trụ cũng khá là đơn giản.
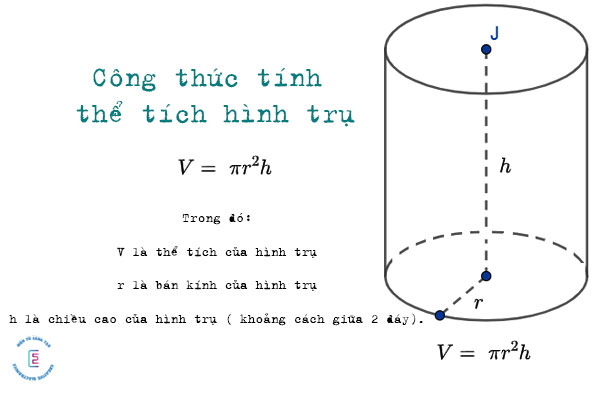
Để có thể tích được thể tích hình trụ thì bạn cần lấy chiều cao nhân với bình phương độ dài bán kính của hình tròn mặt đáy của hình trụ và nhân với Pi.
Công thức tính thể tích hình trụ:
V = . r2 . h
Trong đó:
V là thể tích của hình trụ
r là bán kính của hình trụ
h là chiều cao của hình trụ ( khoảng cách giữa 2 đáy).
Khái niệm về mặt trụ, hình trụ và khối trụ
Ngoài việc bạn cần nhớ công thức tính thể tích hình trụ thì bạn cần phải chú ý thêm một số khái niệm liên quan tới mặt trụ, hình trụ và khối trụ.
Khái niệm về mặt trụ
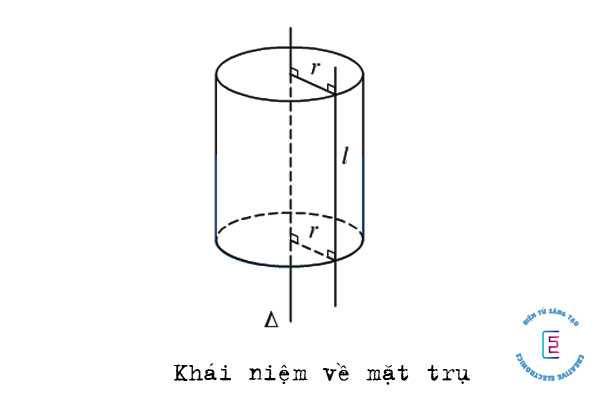
Mặt trụ được biết đến là hình tròn xoay được sinh ra bởi đường thẳng l khi xoay quanh 1 đường thẳng Δ song song và Δ nằm cách 1 khoảng R (Δ là trục), R là bán kính và l là đường sinh.
Ngoài ra, mặt trụ còn được định nghĩa với cách khác là tập hợp tất cả những điểm nằm cách đường thẳng Δ cố định 1 khoảng với bán kính R không đổi.
Hình trụ
Hình trụ là hình được giới hạn ở mặt trụ và 2 đường thẳng song song bằng nhau. Đồng thời chúng cũng là giao tuyến của mặt trụ và 2 mặt phẳng nằm vuông góc với trục.
Ngoài ra, chúng ta có thể hiểu hình trụ chính là hình tròn xoay khi sinh bởi 4 cạnh của 1 hình chữ nhật khi hình chữ nhật quay quanh một đường trung bình của hình chữ nhật đó.
Khối trụ
Bạn có thể hiểu đơn giản, khối trụ chính là hình trụ cùng với phần bên trong của hình trụ đó. Thể tích của khối trụ chính là phần không gian mà hình trụ sẽ chiếm.
Công thức tính Sxung quanh và chiều cao
Để có thể giải được những bài toán phức tạp hơn thì ngoài việc sử dụng những số liệu có sẵn ở đề bài thì bạn cần phải áp dụng các phương pháp tính toán khác để tính ra được các dữ kiện để tính thể tích hình trụ.
Công thức tính diện tích xung quanh (Sxung quanh)
Diện tích của hình trụ được biết đến là toàn bộ phần không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích của 2 đáy.
Ta xét diện tích xung quanh của hình trụ tròn chỉ bao gồm phần diện tích mặt xung quanh, bao quanh trụ tròn và không bao gồm diện tích đáy. Công thức tính diện tích xung quanh hình trụ bằng chu vi đường tròn đáy nhân với chiều cao.
S xung quanh = 2.π.r.h
Trong đó:
r là bán kính của hình trụ
h là chiều cao tính từ đáy tính đỉnh trụ.
Công thức tính chiều cao khi biết S xung quanh
Chiều qua của hình trụ được biết đó chính là khoảng cách của 2 đáy. Công thức sẽ được tính khi biêt được diện tích xung quanh.
S xung quanh = 2.π.r.h
Từ đó ta có thể suy ra được ra chiều cao h.
Bài toán ứng dụng công thức tính thể tích hình trụ
Bài tập 1: Tính thể tích của hình trụ khi biết bán kính của 2 mặt đáy là 7.4 cm với chiều cao là 6 cm.
Lời giải:
Áp dụng công thức tính thể tích hình trụ: V = . r2 . h
Ta có: V = 3.14 x (7.4)2 x 6 = 1031.67 cm3.
Bài tập 2: Tính chiều cao và thể tích của hình trụ, biết chu vi đáy bằng 22 cm, diện tích xung quanh bằng 16 cm2.
Lời giải:
Ta có chu vi đáy của hình trụ cũng là chu vi của hình tròn C hình tròn = 2.r. = 22 cm.
Áp dụng công thức tính diện tích xung quanh hình trụ
S xung quanh = 2..r.h mà 2.r. = 22,
⇒ S xung quanh = 20 x h ⇔ 16 = 22 x h
⇔ h = 16/22 = 0.72 cm
Ta lại có:
2.r. = 22 ⇒ r = 3,5 cm
Áp dụng công thức tính thể tích hình trụ V = . r2 . h, ta có:
V = 3.14 x (3.5)2 x 0.72 = 27.7 cm3
Bài tập 3: Tính diện tích hình trụ biết hình trụ có diện tích xung quanh là 22 cm2 và 30 cm2.
Lời giải:
Áp dụng công thức tính diện tích toàn phần ta có S toàn phần = S xung quanh + Sđáy = 2πrh + 2πr²
2πr² = 30 – 22 = 8
⇔ 2πr² = 8 ⇔ r² = 8 / 2π = 4 ⇔ r = 2
Áp dụng công thức tính diện tích xung quanh hình trụ ta có S xung quanh = 2πrh
⇔ 22 = 2π.2.h ⇔ h = 5.5 cm
Áp dụng công thức tính thể tích hình trụ ta có V = π.r².h = π x 4 x 5.5 = 22π cm3.
Trên đây là một số kiến thức lý thuyến về bài tập áp dụng với công thức tính thể tích hình trụ mà bạn có thể tham khảo. Hy vọng, với những thông tin trên sẽ giúp ích cho bạn trong quá trình học tập.