Phương trình tiếp tuyến được biết đến là một dạng toán được sử dụng rất nhiều trong các đề thi THPT Quốc Gia. Đây là dạng toán đơn giản và thường là phần để giúp cho các thí sinh gỡ điểm. Vì vậy trong quá trình học tập các bạn cần phải nắm rõ kiến thức này. Hãy cùng chúng tôi tìm hiểu về phương trình tiếp tuyến và những bài tập liên quan thông qua nội dung dưới đây của bài viết.
Phương trình tiếp tuyến của đồ thị hàm số
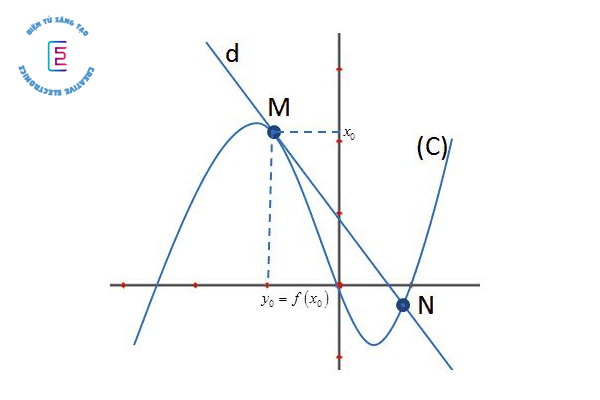
Ý nghĩa của hình học đạo hàm phương trình tiếp tuyến như sau:
Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị C của hàm số tại điểm M(x0,y0). Khi đó thì phương trình tiếp tuyến của C tại điểm M với tại độ (x0,y0) sẽ là: y = y'(x0) (x-x0) + y0.
Nguyên tắc để có thể thiết lập được phương trình tiếp tuyến là phải tìm được hoành độ của X0.
Các dạng bài tập và phương pháp giải phương trình tiếp tuyến
Phương pháp giải toán
Bài toán số 1: Biết hoành độ tiếp điểm x = x0. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x).
Cách giải:
Tính y0= f(x0).
Tính đạo hàm của hàm số ⇒ f’ (x0 )
⇒Phương trình tiếp tuyến: y- y0= f’(x0) ( x- x0)
Bài toán số 2: Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) tại điểm M(x0; f(x0)).
Cách giải:
Tính đạo hàm của hàm số y= f(x).
Từ đó ⇒ f’( x0).
Tiếp tuyến của đồ thị hàm số y= f(x) tại M( x0;y0) là:
y- y0= f’(x0) ( x- x0)
Bài toán số 3: Biết tung độ tiếp điểm bằng y0.Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x).
Cách giải:
Gọi M(x0; y0) là tiếp điểm
Giải phương trình f(x)= y0 ta tìm được các nghiệm x0.
Tính đạo hàm của hàm số ⇒ f'(x0)
Từ đó ⇒ Phương trình tiếp tuyến của đồ thị hàm số.
Bài tập trắc nghiệm phương trình tuyến tính và lời giải
Bài tập 1: Cho hàm số y= x2 + 2x – 6. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là 1?
- y = – 6x + 1.
- y = 4x – 7.
- y = 3x -6.
- y = 2x+1.
Lời giải:
Ta có y(1) = 12 + 2.1 – 6 = -3
Đạo hàm của hàm số đã cho là: y’(x) = 2x + 2
⇒ y’(1) = 2.1 + 2 = 4
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 là:
y + 3= 4( x- 1) hay y = 4x – 7
Đáp án – B đúng
Bài tập 2: Cho hàm số y = x3 + 4x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2?
- y = 4x + 1
- y = 6x + 1
- y = 4x + 2
- y = – 3x + 1
Lời giải:
Xét phương trình: x3+ 4x + 2
⇔ x3+ 4x = 0 ⇔ x = 0
Đạo hàm của hàm số đã cho là: y’ = 3x2 +
⇒ y’(0) = 4
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2:
y – 2 = 4( x – 0) hay y = 4x + 2
Đáp án – C đúng
Bài tập 3: Cho hàm số y= x2– 3x+ 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm của đồ thị hàm số với trục hoành ?
- y= x + 1 và y= – x + 3
- y = – 2x + 1 và y = x- 2
- y= x + 3 và y= – x + 2
- y = -x + 1 và y = x – 2
Lời giải:
Giao điểm của đồ thị hàm số đã cho với trục hoành là nghiệm phương trình : x2– 3x+2 = 0
Vậy đồ thị của hàm số đã cho cắt trục hoành tại hai điểm là A( 1; 0) và B( 2; 0).
Đạo hàm của hàm số đã cho: y’= 2x- 3
+ Tại điểm A( 1; 0) ta có: y’( 1)= – 1
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại A là: y – 0 = -1( x-1) hay y = – x + 1
+ Tại điểm B( 2; 0) ta có y’( 2) = 1
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại B là :
y – 0 = 1( x – 2) hay y = x- 2
Vậy có hai tiếp tuyến thỏa mãn là: y = -x + 1 và y = x – 2
Đáp án – D đúng
Bài tập 4: Cho hàm số y = x4 + 2x2 + 1 có đồ thị ( C). Gọi d là tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ nguyên dương nhỏ nhất. Đường thẳng d song song với đường thẳng nào?
- y = 8x
- y = – 6x
- y = – 10x
- y = 12x
Lời giải:
Đạo hàm của hàm số đã cho là: y’= 4x3+ 4x
Số nguyên dương nhỏ nhất là 1. Ta viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là 1.
Ta có: y’(1 ) = 8 và y(1) = 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số ( C) tại điểm có hoành độ là 1 là:
y- 4 = 8( x- 1) hay y = 8x- 4
⇒ Đường thẳng d song song với đường thẳng y = 8x
Đáp án – A Đúng
Bài tập 5: Phương trình tiếp tuyến của đồ thị hàm số y = ( x- 1)2 ( x- 2) tại điểm có hoành độ x= 2 là
- y = – 2x- 1
- y = x – 2
- y = x + 1
- y = 3x + 1
Lời giải:
Gọi M(x0 ; y0) là tọa độ tiếp điểm.
Từ x0 = 2 ⇒ y0 = 0
Ta có : y = (x-1)2( x-2)= ( x2– 2x + 1) ( x – 2)
Hay y= x3– 4x2+ 5x- 2
⇒ Đạo hàm của hàm số đã cho là : y’= 3x2 – 8x + 5
⇒ y’(2)= 1
Vậy phương trình tiếp tuyến cần tìm là :
y – 0= 1( x- 2) hay y= x- 2
Đáp án – B đúng
Phương trình tiếp tuyến và những bài tập liên quan đã được Điện tử sáng tạo VN giới thiệu đến bạn. Hy vọng, với những thông tin trên sẽ giúp ích cho bạn trong quá trình học tập. Chúc bạn học tập đạt kết quả tốt.